线性表的定义
线性表是一个具有相同特性的数据元素的一个有限序列
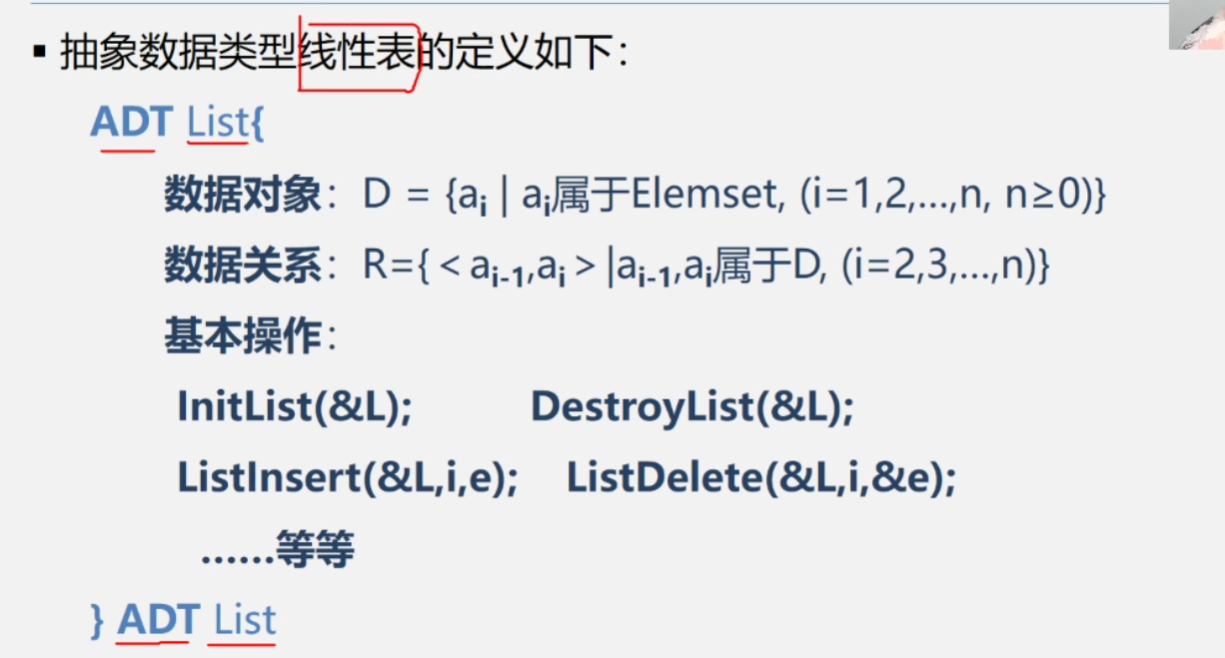
线性表的顺序存储表示
顺序存储:把逻辑相邻的数据存储在物理相邻的存储单元中的存储结构
需要依次存储,中间不能空出存储单元(地址要连续)
顺序表中元素存储位置的计算
假设线性表中,每个元素需要占用 L个存储单元,则有:
LOC(ai)=LOC(a1)+(i-1)*L
线性表的实现
typedef struct{
ElemType *data; //线性表存储空间基址(一个数组)
int length; //当前长度
}SqList;以下是一个例子
#define LIST_INIT_SIZE 1000 //线性表存储空间的初始分配量
typedef struct{ //多项式非零项
float p; //系数
int e; //指数
}Polynomial;
typedef struct{
Polynomial *elem; //线性表存储空间基址
int length; //多项式中当前项的个数
}SqList; //多项式的顺序存储结构类型为SqList
以下是其逻辑结构与存储结构的关系
以下是算法中常用的预定义变量和类型,接下来的代码会用到
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef char ElemType;线性表的基本操作的实现
线性表的初始化、销毁、清空、求长度、判断为空或与取值
typedef struct{
ElemType *elem; //线性表存储空间基址
int length; //多项式中当前项的个数
}SqList; //多项式的顺序存储结构类型为SqList
//初始化
Status InitList(SqList *L){
L->elem = (ElemType *)malloc(LIST_INIT_SIZE * sizeof(ElemType)); //MALLOC分配存储空间
if(!L->elem){ //分配失败
return OVERFLOW;
}
L->length=0;
return OK;
}
//销毁
void DestoryList(SqList *L){
if(L->elem){
free(L->elem);
}
}
//清空
void ClearList(SqList *L){
L->length=0; //从逻辑上的清空,把lenth设为0,则以后的操作都会被拒绝,等同于每个元素都为空的效果
}
//求表的长度
int GetLength(SqList *L){
return L->length;
}
//判断线性表L是否为空
int IsEmpty(SqList *L){
if(L->length==0){
return 1;
}else{
return 0;
}
}
//顺序表的取值
Status GetElem(SqList *L,int i,ElemType *e){ //传入的i是逻辑上的位置从1开始
if(i<1||i>L->length){
return ERROR;
}
e=L->elem[i-1]; //所以要i-1获取存储中的位置
return OK;
}顺序表的查找
从L中查找与给定值e相同的元素数据的位置
int LocateElem(SqList *L ,ElemType *e){
for(int i=0;i<L->length;i++){
if(L->elem==e){
return i+1;
}
}
return 0;
}
顺序表的插入
//顺序表的插入
Status ListInsert(SqList *L,int i,ElemType e){
if(i<1||i>L->length+1){ //i的值不合法
return ERROR;
}
if(L->length==LIST_INIT_SIZE){ //顺序表已经满了
return ERROR;
}
for(int j=L->length-1;j>i-1;j--){ //在存储单元中的下标都是比逻辑的位置小1
L->elem[j+1]=L->elem[j]; //j则被初始化为最后一个元素的存储位置
//直到要插入的逻辑位置的存储位置
}
L->elem[i-1]=e;
L->length++;
return OK;
}

顺序表的删除
Status ListDelete_Sq(SqList *L,int i){
if(i<1||i>L->length){
return ERROR;
}
for(int j=i;j<=L->length;j++){ //初始化为j表示在存储单元中要删除的逻辑位置的数据元素的前一个
//直到表中第一个存储单元中空白的元素
//逐个向前覆盖
L->elem[j-1]=L->elem[j];
}
L->length--;
return OK;
}
以上两种操作 都可以通过画图的方式清晰的理解。